By Sophie Zhu
Invariants are attributes of a mathematical object that stay constant if one changes certain, non-central features. Typically, the features that can be changed are the less distinguishing ones, or the ones that are not innate qualities of the object. The most common way to express invariants are through integral values written as the sum, product, etc. of the values for those non-central features.
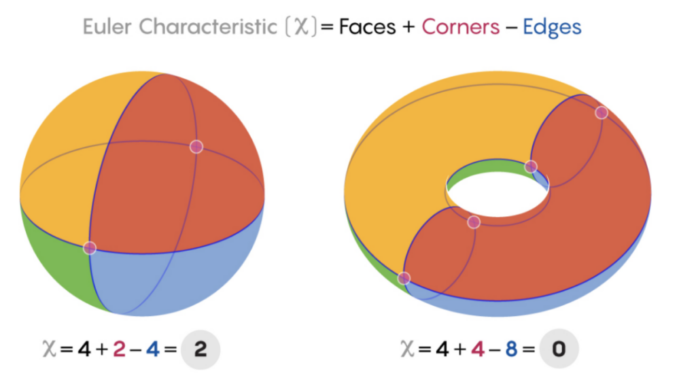
For example, in topology, Euler’s characteristic can be written as the sum and difference of a few features of a certain object. Say we take a torus (a donut) and stretch a triangular net onto it such that no two triangles overlap and the net covers the entirety of the donut. Then we can determine the number of vertices, edges, and faces for that particular torus as follows: characteristic = faces + vertices – edges. What makes the Euler characteristic an invariant is that no matter what netting you choose (you could break up the netting below into a finer one, with more triangles and thus faces, vertices, and edges), the characteristic remains the same. This way, given the Euler characteristic of an object, we can essentially determine what it looks like. In particular, if we stretch the torus below and make it less circular and wider in one direction, it will still have the same Euler characteristic.
In addition, all topological surfaces have a value called its genus, which is basically the number of holes it has (so a torus would have 1 hole). Surprisingly, the Euler characteristic can always be written in terms of the genus: characteristic = 2 – 2 * genus. This further reinforces the idea of one being able to derive the object’s shape from its Euler characteristic.
Invariants are not specific to topology. In combinatorics, many games can be solved with the use of invariants—for example, in the chessboard problem that asks you if it is possible to title an 8-by-8 chessboard having 2 opposite corners removed, with only 2-by-1 dominoes, one notices that each domino covers a white and a black square. Thus, the difference of the number of white and black squares is 0. However, removing the two corners means that the difference should be 2 (since the two corners have the same color), creating a contradiction and showing that it is indeed not possible.
This strategy was used in Lisa Piccirillo’s proof that the Conway knot was slice. Mathematicians attempted to compare the Conway knot to other knots whose slice status was already known using invariants, but the Conway knot eluded them. So, Piccirillo found a detour around this by discovering a knot of her own that she proved was not slice, comparing it to slice-status-known knots using the Rasmussen s-invariant. By showing that her knot and the Conway knot had the same slice status, she discovered a brilliant proof to a decades-old problem.