Sophie Zhu
Number theory is one of the fundamental subject areas in mathematics today. In the most elementary sense, it studies the relations between integers—the whole numbers: 1, 2, 3, etc. Although much of elementary number theory accomplishes that, much of these seemingly simple problems in number theory must be solved using complicated methods over structures called groups, rings, and fields.
In short, groups, rings, and fields are certain types of collections of elements—just like any other set you may know about. However, they also carry operations, like classic addition or multiplication. For example, in a group G with the operation *, for any elements a, b, and c in G, we must have
1. a * b is in G
2. there is an element 0 such that 0 * a = a * 0 = 0
3. (a * b) * c = a * (b * c)
4. there is an element d in G such that a * d = d * a = 0
In rings, it’s nearly the same concept except we have 2 operations, instead of just 1. A field is simply a special case of a ring where each nonzero element has a multiplicative inverse. Namely, there is an element e such that a * e = e * a = 1.
Now, we can use groups, rings, and fields to help solve certain equations called Diophantine equations. In number theory, a Diophantine equation is an equation in a few variables, say x, y, and z, with all integer coefficients. The goal is to find all the integer solutions to those types of equations. Surprisingly, this question can be incredibly difficult for certain types of Diophantine equations, the most notorious of which is Fermat’s last theorem which was recently proved by Andrew Wiles.
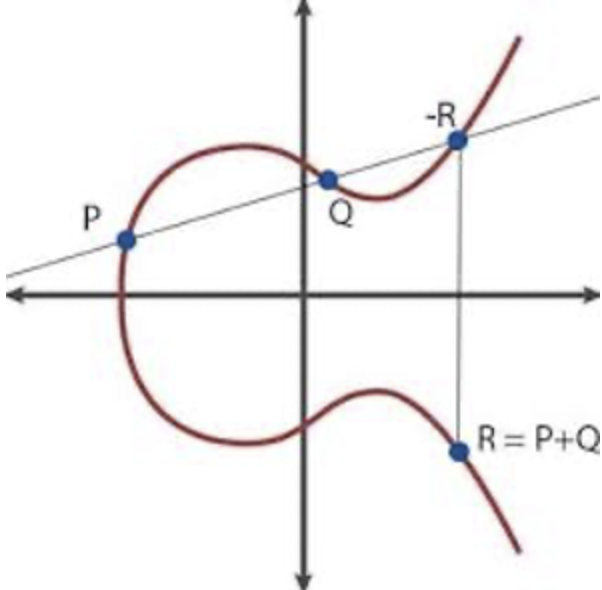
To do this, number theorists often use elliptic curves. They are exactly what they sound like—curves in the plane with equations of the form y2 = x3+ax2+bx+c. What is most intriguing about elliptic curves is that the set of points on an elliptic curve can always form a group, with a very peculiar operation. Namely, the operation * is defined as x * y = the reflection of the point P over the x-axis, where P is the intersection of the line formed by x and y, and the curve. The reason this operation works out is because P always exists—the equation is of form y2 = x3+ax2+bx+c, so any line always crosses through 3 points of the curve (however, there are certain cases where a point can “repeat” itself…but we won’t get into this).
The first thing considered when taking a group is the structure of that group. The process is similar to examining a book; you may inspect the order of the chapters, the way the exercises are organized, and so on. So, for a group, there are indeed several theorems out there that can classify certain groups. For abelian ones—the ones where the operation is commutative, namely, a + b = b + a— a group’s structure can always be uniquely determined. Now, the structure of the group is determined by something even more specific—order. The order of any element a in a group G is the smallest positive integer n such that a + a + … + a = 0 (a is added n times). So, for very special groups called cyclic groups, any element of that group G can be written as g + g + … + g (k number of times) for a fixed G and some integer k.
With groups of elliptic curves, the Nagell-Lutz theorem identifies the structure of the finite part of the group, and the Mordell-Weil theorem identifies the structure of the infinite part. More specifically, Nagell-Lutz tells you a concise way of determining the order of any element in the group with finite order (namely, there exists a finite integer n such that n * a = 0), whereas Mordell-Weil gives the structure of the entire group—including the infinite parts.
The groups of elliptic curves are analogous to many important groups in number theory that enable mathematicians to solve Diophantine equations or study other properties of the integers. The most prominent example is the extensive use of elliptic curves in Weil’s proof of Fermat’s last theorem.